The other area that still holds fascination is how energy is redistributed in biological molecules and how energy is channeled into biological functions. This problem is all the more amazing given the enormous number of atoms involved in the process and the extremely high vibrational density of states by which the energy can be partitioned. In this regard, the great mismatch in vibration density of states and small active space for biological functions is reminiscent to the interfacial charge transfer problem discussed above. How in the world does the energy ever finds its way to a narrow region in nuclear configuration space that would constitute a function or biologically relevant motions? The problem is akin to Levinthal’s paradox in trying to understand how proteins spontaneously find their active structure given the astronomical number of possible, nearly degenerate, nuclear configurations. The coupling of chemical forces to biological processes is an equivalent problem in how these structures actually function and could be considered to be an even more important mystery to solve than the protein’s propensity to find conformational minima with respect to static structure. Life involves movement and we did not have a sound basis to understand how to couple energy into biologically relevant motions.
We started this research area after a brief conversation between RJDM and George McLendon on how vibrational energy flows in large molecules to the surroundings. Even this well-defined problem was not well understood at the time (circa 1985). This discussion was involved the classic drawing on the back of a napkin (at the University of Rochester Faculty Club – the only place to meet for lunch within walking distance…all of the early ideas of RJDM came from chance discussions there.) The Miller group had just developed thermal phase grating spectroscopy using counterpropagating pulses in the UV to get the highest possible time resolution to vibrational energy relaxation into translation motions, the final reservoir or sink for the vibrational relaxation process. The McLendon group had been working on metheme proteins that have very fast excited state relaxation to create excess energy conditions at the heme site that would mimic the excess energy conditions of bond breaking at the heme binding site. This system although quite large would provide an atomic level model for the surroundings in the form of the known structure of the protein matrix, or “solvent”, as a model for vibrational energy redistribution during reactions in solution. The nice feature of this system, as discussed during this eventful encounter, was that all the van der Waals contacts, charge, distances between atoms to understand the energy flow from the active site/chemical hot spot could be very well modelled from the known structure. The rest is history so to speak.
To put the importance of this problem into context, there was considerable discussion on Davidov’s Soliton Model for understanding how energy channeled into biological functions – again in keeping with the Levinthal’s Paradox of protein function. Many biological molecules have helical structures, e.g., DNA, heme proteins, G-protein coupled receptors etc. Davidov’s logic was that there must be reason for the prevalence of these structures, which appear almost spring=like. He proposed that energy in biological systems was highly channeled by these helical, sping-like, conduits to the spatial position involved in barrier crossing or function. The notion of a Soliton requires that the vibrational energy be nondispersive, highly focused, in an undamping manner in these biological canals much like the original observation of undamped water waves in canals with proper excitation (water displacement by a boat at the right speed). This model required energy flow to be nondispersive, undamped, but then how would it be coupled into the function in the first place? Nevertheless, the Soliton concept captured a lot of proponents for this idea.
The very first direct observation of vibrational energy relaxation into translation degrees of freedom to model solution phase processes was the work of Genberg et al, which achieved 10-20 ps time resolution to observing this final relaxation channel. The results were rather amazing rather than some long lived relaxation process, if nondispersive Soliton excitation was involved, all (>90%), of the energy was dissipated into translational degrees of freedom in the surrounding water within 20 ps (modeled as an exponential decay process with this 1/e decay time). Rather than a significant nondispersive relaxation process, the vibrational relaxation occurred on the fastest time scale possible. In fact, if it was just the heme group in contact with water directly, the vibrational cooling would have taken several 10’s of picoseconds to cool the heme group as the water layer would heat up, reach the same (V,R) temperature as the vibrational excited heme (excited state nonradiative relaxation for metheme from excited state to ground state vibrations on the heme group occurs within 100 fs) and there would be no net flow until the vibrational energy could undergo collisional exchange and diffusive motion to next water solvation shell etc. This work illustrated that the excess vibrational energy of the heme, leading to larger rms motions of vibrational modes, coupled to the surrounding heme protein matrix on subps timescale. The energy must have been highly spatially distributed to show up as translational motions of excited waters on such a fast timescale. This observation was the first implication of the important role of collective modes in energy redistribution of biological systems. The coupling of excited vibrations to low frequency collective modes of the surrounding protein increased the effective surface area in contact with the surrounding water and dramatically accelerated V-T collisional exchange with the surrounding waters. This work also served to understand vibrational energy relaxation in the high density of states limit in general. We were heavily influenced by the work of Dana Dlott (U. Ill. Urbana) on this topic but in relation to solid state molecular systems. This body of work was reviewed in Ann. Rev of Phys. Chemistry 1991.
We were now facing a bigger conundrum as we found that energy was extremely rapidly dispersed in biological systems. The problem with the Davidov Soliton concept is that all the vibrational modes would need to excited in phase to interfere constructively and not undergo dissipation (this point was never discussed by Davydov or its propoonents). These modes were mathematically treated as undamped. The above work showed the fundamental flaw in the Davidov model. The high frequency vibrations relax on intramolecular vibration redistribution (IVR) timescales (100 fs timescale) in the high density of states limit to low frequency modes. The lowest frequencies modes of the surrounding protein are collective helical motions, that from noted timescale for collisional exchange with water into translational degrees of freedom must be highly damped. How then do biological molecules work?
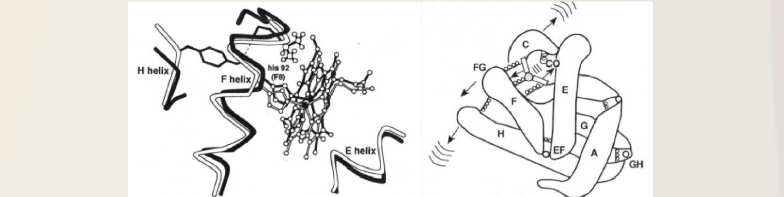
The answer came a couple of years later when the biologically relevant protein motions were studied with the same phase grating method but now studying the protein motions involved with ligation at the heme site using carboxy myoglobin (MbCO) and hemoglobin (HbCO) as the model system for oxygen binding/dissociation. This system was chosen as it has a 100% quantum yield for dissociation with no rebinding; so the entire pathway of motions assisting bond breaking to ligand escape out of the protein could be studied. Initially the hope was to measure the energetics of the Fe-ligand (CO) bond and barriers to ligand escape. The big surprise was that there was a much bigger acoustic wave launched that that observed for purely vibrational/thermal relaxation processes and the motions involved still persisted at the zero thermal expansion point for water. The motions and timescales match the time required for the helical motions, EF helices in particular, and was the first observation of collective modes involved in biological processes (Genberg et al Science 1991). This concept has since been confirmed for a number of biological systems. Further work by Goodno et al with the ultimate limit in sensitivity achieved using heterodyne detection of the pure phase component showed the motions were anisotropic and were highly directing the forces from the bond dissociation to collective motions of the surrounding helices. (Higher excitation or heating led to an isotropic response or loss of functional directionality). We also showed that the motions were corelated from the very fastest motions with 4 fs time resolution (a record at the time) to observe the porphyrin ring modes that allow the iron to move out of the heme plane upon bond dissociation to channel this force into the helical motions. We showed that the time scale of motions was correlated over different length scales to prove the response was collective.
This work solved how energy redistribution occurs from a localized chemical reaction and is transduced into biological functions by coupling to collective modes. Using heme proteins as conceptual basis, it is the tertiary helical motions of the individual heme proteins in hemoglobin that change the binding of the quaternary contacts and lead to the motions affecting the allosteric control of oxygen binding as part of oxygen transport in the body. The state of ligation at one heme binding site is communicated to adjacent proteins by collective helical displacements at the speed of sound. Effectively, through this mechanism, there is a through space coupling of reaction coordinates by which the state of ligation affects a neighbouring heme protein. This mechanism is important as the functionally relevant motions employed by hemoglobin in the transport of oxygen in the body serves as our cornerstone for understanding allosteric regulation and molecular cooperativity. This chemical communication simply could not be faster or more efficient. It is a beautiful thing to behold as this process is so energetically efficient.
This work led to the proposal of the collective mode coupling model for explaining how biological systems exploit chemical processes to drive biological functions. The historical background and basic concepts are explained in Energetics and Dynamics of Deterministic Protein Motion. R. J. Dwayne Miller, Acc. Chem. Res. 1994, 27, 5, 145–150 and an extended overview given in the J. C. Polanyi Award (2000) Lecture, “Mother Nature and the Molecular Big Bang, Can. J. Chem. Vol. 80. (1) 2022, https://doi.org/10.1139/v01-199. This new conceptual basis explains how the enormous number of nuclear degrees of freedom become spatially correlated by secondary and tertiary structures to highly direct chemical forces into biological processes, on time scales faster than the energy redistribution processes or simply heating. It is an amazing feat of molecular engineering.
The collective mode coupling model explains how chemical forces/energy can be highly directed despite biological systems exhibiting strong system-bath coupling imbedded in highly damped lattice, as presented by the protein matrix or other biological structure. The question now becomes what are the specific collective motions that act as conductors for the “biological orchestra of sound” giving rise to living systems? This newly posed question at the time was the driving force for the group to develop ultrabright electron sources to literally light up a atomic motions to directly observe the very essence of chemistry. There is a conceptual basis waiting to be discovered in the form of topological structures that nature has discovered over time to highly direct chemistry. It is now clear collective helical motions are involved but it may well be that the highly disordered loops or liquid like domains in protein structure, that give proteins their flexibility, are the most important structural elements. It is the loop like domains that impart fluidity to proteins so that despite being highly associated systems are not glasses at room temperature. (This idea is in contrast to ideas of conformational substates and hierarchical basis using glass models for protein dynamics.) These topological elements and how to pattern them will be the new “periodic table” of life.
It should be noted here that the concept of collective mode coupling has now been established and it is worth pointing out its origins. The question now relates to the specific length scales for the spatial correlation imposed by the protein structure. This question has now been answered by the Schlicting group (Bioarchives 2022) in which they were the first to observe biologically relevant motions within the linear response (1-photon excitation per chromophore) to show the importance of these motions and were able to pull out the spatial correlations, that do not involve the whole helix, but rather a more localized section to further focus reaction forces. We are starting to see our first glimpses of how the collective mode coupling works and how Nature is wired up.